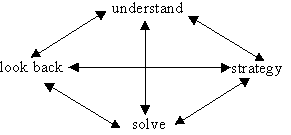
On this page we discuss "What is Problem Solving?" under the 3 headings:

Introduction     Four Stages of Problem Solving       Scientific Approach

Introduction

Naturally enough, Problem Solving is about solving problems. And we’ll restrict ourselves to thinking about mathematical problems here even though Problem Solving in school has a wider goal. When you think about it, the whole aim of education is to equip children to solve problems. In the Mathematics Curriculum therefore, Problem Solving contributes to the generic skill of problem solving in the New Zealand Curriculum Framework.

But Problem Solving also contributes to mathematics itself. It is part of one whole area of the subject that has largely passed unnoticed in schools around the world. Mathematics consists of skills and processes. The skills are things that we are all familiar with. These include the basic arithmetical processes and the algorithms that go with them. They include algebra in all its levels as well as sophisticated areas such as the calculus. This is the side of the subject that is largely represented in the Strands of Number, Algebra, Statistics, Geometry and Measurement.

On the other hand, the processes of mathematics are the ways of using the skills in new and creative ways. Problem Solving is a mathematical process. As such it is to be found in the Strand of Mathematical Processes along with Logic and Reasoning, and Communication. This is the side of mathematics that enables us to use the skills in a wide variety of situations.

Before we get too far into the discussion of Problem Solving, it is worth pointing out that we find it useful to distinguish between the three words "method", "answer" and "solution". By "method" we mean the means used to get an answer. This will generally involve one or more problem solving strategies. On the other hand, we use "answer" to mean a number, quantity or some other entity that the problem is asking for. Finally, a "solution" is the whole process of solving a problem, including the method of obtaining an answer and the answer itself.

method + answer = solution

But how do we do Problem Solving? There appear to be four basic steps. Pólya enunciated these in 1945 but all of them were known and used well before then. And we mean well before then. The Ancient Greek mathematicians like Euclid and Pythagoras certainly knew how it was done.

Pólya’s four stages of problem solving are listed below.

Four Stages of Problem Solving                                     Back to Top

1. Understand and explore the problem;
2. Find a strategy;
3. Use the strategy to solve the problem;
4. Look back and reflect on the solution..

Although we have listed the Four Stages of Problem Solving in order, for difficult problems it may not be possible to simply move through them consecutively to produce an answer. It is frequently the case that children move backwards and forwards between and across the steps. In fact the diagram below is much more like what happens in practice.

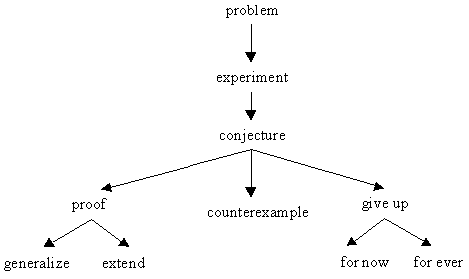
There is no chance of being able to solve a problem unless you are can first understand it. This process requires not only knowing what you have to find but also the key pieces of information that somehow need to be put together to obtain the answer.

Children (and adults too for that matter) will often not be able to absorb all the important information of a problem in one go. It will almost always be necessary to read a problem several times, both at the start and during working on it. During the solution process, children may find that they have to look back at the original question from time to time to make sure that they are on the right track. With younger children it is worth repeating the problem and then asking them to put the question in their own words. Older children might use a highlighter pen to mark and emphasise the most useful parts of the problem.

Pólya’s second stage of finding a strategy tends to suggest that it is a fairly simple matter to think of an appropriate strategy. However, there are certainly problems where children may find it necessary to play around with the information before they are able to think of a strategy that might produce a solution. This exploratory phase will also help them to understand the problem better and may make them aware of some piece of information that they had neglected after the first reading.

Having explored the problem and decided on a plan of attack, the third problem-solving step, solve the problem, can be taken. Hopefully now the problem will be solved and an answer obtained. During this phase it is important for the children to keep a track of what they are doing. This is useful to show others what they have done and it is also helpful in finding errors should the right answer not be found.

At this point many children, especially mathematically able ones, will stop. But it is worth getting them into the habit of looking back over what they have done. There are several good reasons for this. First of all it is good practice for them to check their working and make sure that they have not made any errors. Second, it is vital to make sure that the answer they obtained is in fact the answer to the problem and not to the problem that they thought was being asked. Third, in looking back and thinking a little more about the problem, children are often able to see another way of solving the problem. This new solution may be a nicer solution than the original and may give more insight into what is really going on. Finally, the better students especially, may be able to generalise or extend the problem.

Generalising a problem means creating a problem that has the original problem as a special case. So a problem about three pigs may be changed into one which has any number of pigs.

In Problem 4 of What Is A Problem?, there is a problem on towers. The last part of that problem asks how many towers can be built for any particular height. The answer to this problem will contain the answer to the previous three questions. There we were asked for the number of towers of height one, two and three. If we have some sort of formula, or expression, for any height, then we can substitute into that formula to get the answer for height three, for instance. So the "any" height formula is a generalisation of the height three case. It contains the height three case as a special example.

Extending a problem is a related idea. Here though, we are looking at a new problem that is somehow related to the first one. For instance, a problem that involves addition might be looked at to see if it makes any sense with multiplication. A rather nice problem is to take any whole number and divide it by two if it’s even and multiply it by three and add one if it’s odd. Keep repeating this manipulation. Is the answer you get eventually 1? We’ll do an example. Let’s start with 34. Then we get

34 17 52 26 13 40 20 10 5 16 8 4 2 1

We certainly got to 1 then. Now it turns out that no one in the world knows if you will always get to 1 this way, no matter where you start. That’s something for you to worry about. But where does the extension come in? Well we can extend this problem, make another problem that’s a bit like it, by just changing the 3 to 5. So this time instead of dividing by 2 if the number is even and multiplying it by three and adding one if it’s odd, try dividing by 2 if the number is even and multiplying it by 5 and adding one if it’s odd. This new problem doesn’t contain the first one as a special case, so it’s not a generalisation. It is an extension though. You might like to see if this new problem always ends up at 1. Or is that easy?

It is by this method of generalisation and extension that mathematics makes great strides forward. Up until Pythagoras’ time, many right-angled triangles were known. For instance, it was known that a triangle with sides 3, 4 and 5 was a right-angled triangle. Similarly people knew that triangles with sides 5, 12 and 13, and 7, 24 and 25 were right angled. Pythagoras’ generalisation was to show that EVERY triangle with sides a, b, c was a right-angled triangle if and only if a² + b² = c².

Scientific Approach                                                   Back to Top

Another way of looking at the Problem Solving process is what might be called the scientific approach. We show this in the diagram below.

Here the problem is given and initially the idea is to experiment with it or explore it in order to get some feeling as to how to proceed. After a while it is hoped that the solver is able to make a conjecture or guess what the answer might be. If the conjecture is true it might be possible to prove or justify it. In that case the looking back process sets in and an effort is made to generalise or extend the problem. In this case you have essentially chosen a new problem and so the whole process starts over again.

Sometimes, however, the conjecture is wrong and so a counterexample is found. This is an example that contradicts the conjecture. In that case another conjecture is sought and you have to look for a proof or another counterexample.

Some problems are too hard so it is necessary to give up. Now you may give up so that you can take a rest, in which case it is a ‘for now’ giving up. Actually this is a good problem solving strategy. Often when you give up for a while your subconscious takes over and comes up with a good idea that you can follow. On the other hand, some problems are so hard that you eventually have to give up ‘for ever’. There have been many difficult problems throughout history that mathematicians have had to give up on.