Problem
Ngawai and Tom make a peanut butter sandwich. How can they share it fairly?

Can you find three different ways to cut the sandwich?

What is this problem about?
This problem is about finding equal parts of a whole. A whole can be described as a region or a unit. When there are two equal parts each is a half.

The cuts in this problem have to be made so that each piece is exactly the same as the other. You may therefore need to simplify the problem in the first instance, by imagining that the loaf of bread has a rectangular cross-section.

Encourage the children to find as many ways of solving this problem as they can.

Achievement Objectives
Number (Level 1)
- find by practical means, one half and one quarter of a shape and a half of a set of objects.

Mathematical Processes
- devise and use problem solving strategies (act it out, draw a picture)

Resources
Rectangular pieces of paper
Peanut butter sandwich (to introduce the problem)
Blackline master of the problem

Specific Learning Outcomes
The children will be able to:
- divide a region into two equal parts through folding or cutting
- demonstrate that the two parts are equal and describe these parts as halves

1. Introduce the problem using a peanut sandwich and two children from the class.
2. Ask the children to all think of one way that they could share the sandwich. Share one idea.
3. Read the problem to the class.
4. Solve the problem in pairs. As the children work, ask questions that focus on the meaning of a ½. Allow the children to describe their ideas. Encourage explanations.
   How do you know the parts are equal?
   Are you happy with your share? Why?
   Can you think of other ways to share it?
   Tell me about your thinking?
   How are you keeping track of the ways that you find?
5. Ask that the children keep a record of the different ways that they find to share the sandwich.
6. Share solutions.

Extension Problem
Imagine a loaf that does not have a square cross-section.
Use 4 children instead of 2.
Share a bag of 8 lollies between Ngawai and Tom.

Other Contexts for the Problem
Giant chocolate chip cookies (circular region)
Working space on a desk

Solution
There are, in fact, an infinite number of solutions. As long as you cut or fold through the centre point of the rectangle the parts will be equal. Some examples of single cuts or folds are:
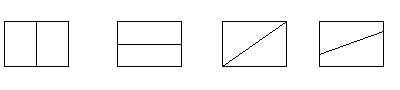
In order to see that all of these cuts do give equal parts, it is enough to put one on top of the other. This may require rotation in some cases. This may provide the opportunity to explore some of the symmetry and transformation ideas from the Geometry Strand.

If the bread has a cross-section that consists of a rectangle with a semi-circle on top, then there is only one simple solution to the problem. There must be a solution by cutting parallel to the base of the rectangle (the side opposite the semi-circle) but it is extremely difficult to find the exact point o make this cut.

Extension: To produce four equal parts is a little more difficult. In the first two drawings above, a second cut perpendicular to the first cut and through the centre will work. As for the other drawings, many solutions exist but in practice they are hard to find.