Problem
Tina and Tom were twins. Tina saves and Tom spends. Tom found a $20 note on Sunday evening and spent $2 a day starting on Monday. Coincidentally, Tina started work that Monday and gets $2.50 a day. How long would it be before Tina has more money than Tom?

What is this problem about?
This problem involves setting up a practical situation to be solved mathematically. It can be done by guess and check or by using a table or in a number of other ways. We’ll do it first of all using a graphical approach and then look at it from an algebraic point of view. It is worth exploring all these ways to see which ones work best. This approach to the problem will give the children ammunition that they can use in other situations. It will also strengthen links for them across the curriculum.

Achievement Objectives
Algebra (Level 4)
- sketch and interpret graphs on whole number grids which represent simple everyday situations
- find a rule to describe any member of a number sequence and express it in words
- use a rule to make predictions.

Mathematical Processes
- devise and use problem solving strategies to explore situations mathematically (guess and check, be systematic, make a drawing)

Resources
Graph paper
Blackline master of the problem (English)
Blackline master of the problem (Maaori)

Specific learning outcomes
The children will be able to:
- describe a rule for continuing a number sequence
- compare two number sequences

1. Pose the problem to the class. You may use 2 children to help establish the problem and interest the class in the problem.
2. Brainstorm for ways to solve the problem – list these on the board for the children to refer to as they solve the problem.
3. As the children work on the problem in pairs ask questions that focus on the strategy they have selected.
   What approach are you using? Why did you select that approach? Are you making progress?
4. Encourage the children to record their solutions in ways that clearly describe what they did.
5. Display and share written solutions.

Extension to the problem
Write you own twins problem for others to solve.

Solution
In the graph below, we sketch the situation. Diamonds represent Tom’s finances and squares represent Tina’s situation.

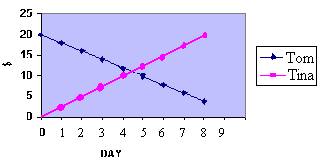
From the graph we can easily see that the small squares go above the crosses on day 5, Friday. So it is five days until Tina has more money than Tom.

Extension: To do this algebraically we first have to find out the two rules for the number patterns produced by Tom and Tina’s activity. Now Tom started off with $20 and then spent $2 a day. So each day he had $2 less. His equation is

M = 20 – 2n.

On the other hand Tina earns $2.50 each day and so her equation is

M = 2.5n.

You should check these equations by putting in actual values for n.
If the two Ms can ever be equal we will have

2.5n = 20 – 2n, which becomes 4.5n = 20, so n is 4 and a bit.