Problem
Six businesspeople meet for lunch and shake hands with each other. How many handshakes are there?

What is this problem about?
The maths that is involved in this problem depends on the approach that is used to solve it. If the children look for patterns starting with the simpler cases (2 people etc) the problem involves triangular numbers.

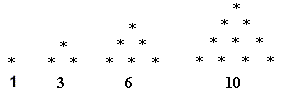
Achievement Objectives
Algebra (Level 3)
- state the general rule for a set of similar practical problems
- describe in words, rules for continuing number and spatial sequential patterns

Mathematical Processes
- devise and use problem solving strategies to explore situations mathematically (systematic list, draw a picture, use equipment).

Resources
Blackline master of the problem (English)
Blackline master of the problem (Maaori)

Specific learning outcomes
The children will be able to:
- use diagrams or lists to show relationships
- identify the pattern of triangular numbers

1. Introduce the problem by getting 3 children to role-play people meeting and shaking hands.
2. Count and record the number of handshakes. Discuss other ways of convincing others that there are 3 handshakes (eg, draw a picture)
3. Pose the problem for the children to work on in pairs or small groups.
4. Brainstorm for ways to solve the larger problem (act it out, make a list and look for a pattern). List these on the board for the children to consider.
5. As the children work ask questions that focus their thinking on working systematically and looking for patterns.
   How are you keeping track of the handshakes? (diagram, list)
   How many handshakes do you think that there would be if you added another person?
   What do you notice about the number of handshakes and the number of people?
   How could you record your work so that you could look for a pattern?
6. Share results.

Extension to the problem
How many handshakes are there at the meeting if people come in pairs and shake hands with everyone except their own partners.

Solution
If two people shake hands there is one handshake.
If three people shake hands there are 3 handshakes.
If four people shake hands there are 3 more handshakes so 3 + 3 = 6 in total.
If five people shake hands there are another 4 handshakes so 6 + 4 = 10.
For 6 people there are another 5 handshakes so 10 + 5 = 15.

A second pattern that may be described is that each person has to shake hands with all the others. If there are 6 people each person has 5 handshakes to make. But each time a handshake occurs there are 2 people involved. This means that you only need ½ (6 x 5 ) = 15.