Problem
Penny’s favourite pizza restaurant offers 6 toppings: ham, onions, mushrooms, pineapple, tomato and peppers. Penny ordered a pizza with ham and pineapple. Unfortunately the server only wrote down that she wanted 2 toppings but didn’t write down what they were. The cook decided to pick two toppings at random.

What is the probability that Penny will get the pizza she ordered?

What is this problem about?
This problem involves working out the probability of an event when the outcomes are equally likely to occur. (In this case each topping is equally likely to be chosen by the chef.) The probability of any particular outcome is:

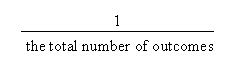
In the problem extension we are interested in a particular set of outcomes. The probability is expressed by the fraction: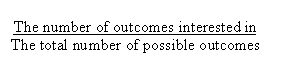

Students should see that any fraction of this type must be between 0 and 1, since the numerator cannot be nehative and cannot be bigger than the denominator. If the set of "outcomes that you are interested in" contains all the possible outcomes, then you are certain to get the result you are interested in, and the fraction is equal to 1. Likewise, an event that is impossible has a probability equal to 0.

The focus is on making a list of possible outcomes as a method for finding probability.

Achievement Objectives
Statistics (Level 4)
- estimate the relative frequencies of events and mark them on a scale

Mathematical Processes
- devise and use problem–solving strategies to explore situations mathematically (make an organised list)

Resources required
Blackline master of the problem (English)
Blackline master of the problem (Maaori)

Specific learning outcomes
The children will be able to:
- make a list of possible outcomes as a method of finding probability

1. Discuss favourite pizza’s as a way to gain interest in the problem.
2. Read the problem with the class.
3. Brainstorm ways to approach the problem. At this point you might be encouraging the children to plan ways to find all possible pizza’s.
4. Children work with a partner on the problem.
   How do you know that you have found all the pizza’s?
   How have you oraganised your search for the pizza’s?
   How many of these pizza’s are what Penny ordered?
5. Share solutions.

Extension
Penny actually likes all the toppings except peppers and mushrooms. What is the probability that she will get a pizza that she likes now?

Solution to the problem
Probably the most common approach is to make a list of all the possible two-topping combinations. Such a list might be organised like:
Ham and pineapple
Ham and tomatoes
Ham and peppers
Ham and mushrooms
Ham and onions

Pinepple and tomatoes
Pineapple and peppers
Pineapple and mushrooms
Pineapple and onions

Tomatoes and peppers
Tomatoes and mushrooms
Tomatoes and onions

Peppers and mushrooms
Peppers and onions

Mushrooms and onions

With the list of 15 pizza’s (5 + 4 + 3+ 2 + 1) , the children will be able to see that Penny has 1/15 chance of getting the pizza she ordered.