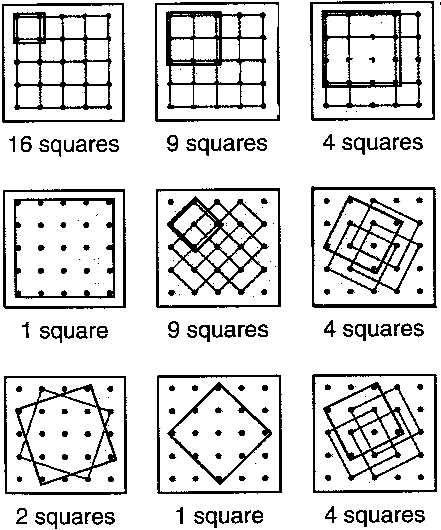
Problem

What is this problem about?
This problem explores the concept of "squareness". It reinforces the
understanding that a square has 4 equal sides and 4 right angles. The children need to
recognise that a square is not always ![]()
but may be![]()
The problem also encourages the children to be systematic in their counting of the various sized squares.
Achievement Objectives
- create and talk about geometric patterns which repeat, or which have rotational or reflective symmetry
Mathematical Processes
- devise and use problem solving strategies (act it out, draw a picture)
- use equipment appropriately
Resources required
Blackline master of problem
Specific learning outcomes
- describe the properties of a square
- work systematically when problem solving
Teaching sequence
- Introduce the problem as a "treasure hunt". How many squares can be made on this board (or grid)? Let the search begin!
- Ask the children, in pairs, to make a square on the geoboard with a rubberband (or draw one on the dot paper). It can be any size and in any location.
- Share the squares found by the class. Notice whether the squares displayed are different by size, location or both.
- Pose the problem: How many squares do you think that you can find?
- As the children work ask:
How do you know when something is a square?
What did you find out during this activity?
Are you organising your search for the squares? How? - Share answers. If there are different answers look at why this is so. Get the children to share the ways that they organised their search.
Extension
Other contexts for the problem
Solution
| Size of square | Number |
| 1x1 | 9 |
| 2x2 | 4 |
| 3x3 | 1 |
| tilted (one dot enclosed) | 4 |
| tilted (4 dots enclosed) | 1 |
Some children may notice that there is a pattern in the number of the non-tilted
squares (1, 22, 32)
Extension:
Solution: