Copycats Geometry, Level 3
Problem
Simon has just discovered copycats. A square is a copycat because you can put four of them together to make another square.
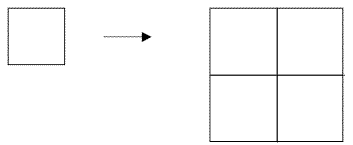
Simon wondered if triangles and circles were copycats. What do you think?
What is this problem about?
This is a simple example that investigates an idea to do with shapes that the children might not have normally met. It should help them explore basic shapes in a creative environment.
The first extension is a novel way to link their knowledge of geometry with patterns. The second extension is also useful in developing children’s thinking skills. For example, in the extension, they have a free rein to create any shapes they like that are copycats.
Achievement Objectives
Geometry (Level 3)
- describe the features of 2-dimensional and 3-dimensional objects, using the language of geometry
- design and make a pattern which involves translation, reflection or rotation
Mathematical Processes
- devise and use problem solving strategies to explore situations mathematically (guess
and check, make a drawing, use equipment)
Resources
squares, circles, triangles
Blackline master of the problem (English)
Blackline master of the problem (Maaori)
Specific learning outcomes
The children will be able to:
- tessellate using squares and triangles
- describe the properties of tessellating shapes
Teaching sequence
- Ask: What is a copycat?
- Discuss the definition of copycat as it applies to this problem.
- Give the children (in pairs) an equilateral triangle and ask them to find out whether it
is a copycat. Discuss the properties of an equilateral triangle (3 equal sides, 3 equal
angles )
How do you know that they are equal? (fold and check) - Share findings.
- Pose the problem: Are all triangles copycats?
The children need to make their own triangle and see if it is a copycat. As they work ask:
What type of triangle are you using? (right triangle, scalene, isoceles, equilateral)
Describe the triangle that you are using?
Are circles copycats? Why do you think that? - Share findings.
Extension to the problem
- Simon talked to Ben about his copycats. Ben noticed that you needed four squares to make a bigger square and four triangles to make a bigger triangle. Could you make a square with any other number of squares? How many squares can you put together to make a square? Is there a pattern here?
- What other shapes are copycats?
Solution
All triangles are copycats. This can be shown using four triangles as in the picture.
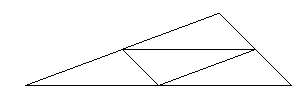
On the other hand, circles aren’t copycats. Having said that we have to prove it. The problem with circles is that when you put two of them together, they don’t fit. Clearly two circles don’t make a circle. So we need three at least. But three circles put together have lots of gaps. So there is no way that three or more circles can be put together to fill up all the space of another circle.
Extension 1: It turns out that 4, 9, 16, 25, and, in fact, any square number of squares can be used. Why can’t a non-square number be used? Is this the same for triangles too or do you have to use triangle numbers there?
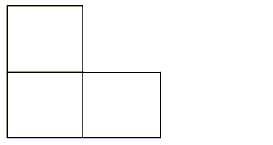
Extension 2: The L-shape in the drawing below is a copycat. To
check this out, put one L-shape around each of the top-left, bottom-left and bottom-right
corners.
Perhaps you could send the new copycats that your class finds.
