Problem
Henry wants to make a rectangular chicken run at the back of the house. He bought 12 metres of fencing wire. What is the largest area run that he can make for his chickens?

What if Henry had 60 metres of fencing?

What is this problem about?
This problem requires children to use a number of problem strategies, to make a number of calculations relating to rectangles, and to compare the results of the area calculations that they have performed.

The problem strategies include drawing a diagram (in order to ‘see’ how the dimensions of a rectangle of fixed perimeter relate to each other), making a table (in order to compare calculations easily) and to be systematic (to make the table entries easier to compare).

Children will also need to know (or will need to learn), the formulae for perimeter of a rectangle and area of a rectangle in terms of its length and width.

After the children have tackled Part B, they should begin to feel that the maximum area of a rectangle is obtained when the rectangle is a square. They should be aware of this when they are attempting the extension. This case should lead them to question whether they should be using whole numbers for the rectangles’ dimensions or decimals.

Achievement Objectives
Measurement (Level 4)
- calculate perimeters of circle, rectangles and triangles, areas of rectangles, and volumes of cuboids from measurements of length

Mathematical Processes
- devise and use problem solving strategies to explore situations mathematically (guess and check, be systematic, make a table, make a drawing)
- use equipment properly

Resources
cm cubes, squared paper
Blackline master of the problem (English)
Blackline master of the problem (Maaori)

Specific learning outcomes
The children will be able to:
- explain the relationship between the area and perimeter of rectangles
- use a table to solve a problem

1. Introduce the problem with a piece of string 12 m long. Ask 4 children to make a rectangle with the string. Discuss its perimeter and how they would calculate its area. Ask another 4 children to make another rectangle – estimate whether the area would be greater or smaller that the first one.
2. Read the problem to the class.
3. Brainstorm ways to solve the problem eg. use equipment (squared paper, cm cubes)
4. As the children work ask questions to focus their thinking on working systematically and looking for the relationship between the perimeter and area.
   What can you tell me about that rectangle?
   How are you keeping track of the rectangles that you are making?
   How do you know that you have found all the possible rectangles?
5. Share findings. Encourage the children to make statements about the area and perimeter of the shapes that they have found. Discuss ways to record the measurements to make it easier to see the relationship (table).
6. Pose the second part of the problem.
7. Before they begin working on the problem, remind them to think about ways of working systematically. Check that they planning how they will record their findings.
8. Share solutions.
9. Encourage the children to make statements about the relationship between perimeter and the rectangle with the largest area.

Extensions to the problem
Repeat the problem above with 14 metres of fencing.

Other contexts for the problem 
Carpet, layout for a model rainway, pig-pen

Solution to the problem
At this Level we would expect children to tackle this problem by working out the area of a number of rectangles and then choosing the dimensions that give the biggest answer.


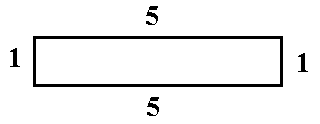
Suppose that Henry decided to have a run that was a rectangular shape with the smallest side being 1 metre long. He now has to work out the dimension of the other side to give a value of 5 metres. The area of this run is 1 x 5 = 5 square metres.

But Henry might have used a side length of 2 metres. In that case his chicken run would have had area 2 x 4 = 8 square metres. Or he might have used a side length of 3 metres to give an area of 3 x 3 = 9 square metres.

Now if Henry moves up to 4 metres along the smallest side he’ll find that the longest side is only 2 metres long. There are two things to notice about this. First the smaller side is longer than the longer side and second, Henry has already dealt with the 2 x 4 rectangle. So Henry realises that he has covered all cases for rectangles with whole number side lengths. Hence the maximum area is 9 square metres.

Second part of problem: Henry has to do considerably more calculations when he has more fencing. It is therefore a good idea to summarise the calculations in table form.

From the table we see that Henry’s largest chicken run has area 225 square metres.

Extension : Some children at this stage might notice that the biggest area in the two examples above occurs when the rectangle is a square. Is this always the case? So let Henry try the 14 metre fencing option.

Henry’s table now uses decimal side lengths and adds in the square case as well. Here the square is again the best option.