The Castle                                              Geometry, level 4

Problem
Ravi has designed plans for a castle that show the front, top, and side views.

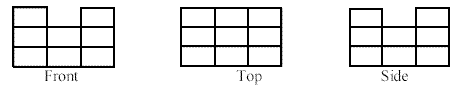
Build a castle to Ravi’s design using the cubes.
What is the largest number of cubes that you can use in the construction of a castle from Ravi’s plans?
What is the smallest number of cubes that you can use in the construction of a castle from Ravi’s plans?
Can you build a symmetrical castle that is different from any of the ones you have built so far? How many symmetrical castles can you build to the Ravi’s specifications?

What is this problem about?
This problem explores the relationship between 2-D and 3-D shapes and helps to visualise 3-D shapes from 2-D representations. It shows that different 3-D objects can be represented by the same set of 2-D objects. The problem also investigates the symmetry of objects.

Achievement objectives
Geometry (Level 4)
- make a model of a solid object from diagrams which show views from the top, front, side and back; describe the reflection or rotational symmetry of a figure or object

Mathematical Processes
- devise and use problem solving strategies to explore situations mathematically (guess and check, use equipment)

Learning outcomes
The children will be able to:
- Construct 3-D shapes from 2-D drawings
- Describe the symmetries of 3-D shapes
- Draw 3-D shapes on isometric paper

Resources required
small cubes
isometric dot paper
Blackline master of the problem (English)
Blackline master of the problem (Maaori)

Teaching sequence

1. Introduce the problem – create a scenario that the children are builders who have been given the task of constructing a castle from a set of plans. Make sure that the children understand how to use the 2-D views and the isometric paper.
2. Give blocks and isometric paper to pairs of children.
3. As the children work ask questions that focus their thinking on the models they are building.
   What does the view from the top of your model look like? Side?
   Is there any way to use the blocks to get the same view?
   How do you know if you have found all the possibilities?
   Is your castle symmetric? Describe.
   What advice would you give someone about drawing with isometric paper?
4. Share solutions – both models and isometric drawings.

5. If you are using this problem to reinforce symmetries require that the children record the symmetries on the drawing or describe them.

1. Is it possible to design plans for a castle so that it can only be built in one way (uniquely)?
2. On a base of three cubes by three cubes, design your own construction using top, side and front views only. Ask the questions above about your design. Stick to a three by three base. What design will give you the biggest difference between the largest number of cubes you can use and the smallest number?

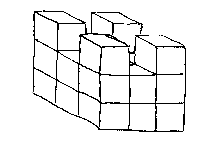
Here we show one possible castle that could be drawn from Ravi’s design.

This castle looks exactly the same from each side. It has 22 blocks.

Actually this is the most blocks that can be used for Ravi’s design. If any other block is added, there will either be three consecutive blocks across a ‘face’ of the castle or there will be an extra block right in the middle of the top layer. Either of these situations can only occur if either the front or side views look like B. So no more blocks can be added.

There may be some dispute as to what constitutes the smallest castle. Here we assume that there have to be 9 blocks on the base. Given that, we have shown the smallest number of cubes in the castle below. It is assumed that the castle looks the same from the corner block opposite the nearest block.

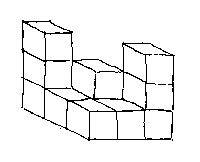By having ‘towers’ in opposite corners the castle has the correct front and side views. This castle has 14 blocks. Is this the only smallest castle?

It is possible to build other symmetrical castles. Just add the same tower to the two opposite corners that only have one block in the picture above. This tower can have one block in it or two. The version with two blocks has more symmetry than the other one. There are other possibilities too. How many can you find? (Fax us your solutions)